Die Hersteller namhafter CFD Softwarepakete geben sich Mühe, die jeweiligen Vorteile ihrer Software gut in Szene zu setzen. Dabei bemühen sie Begriffe wie „zuverlässig“, „genau“, „schnell“, „robust“, „einfach“, etc. . Aber was heißt das im konkreten Anwendungsfall? Und ist schnell nicht auch ungenau?
Die Nachteile finden dabei selten den Weg in die Marketingkanäle oder können wenn überhaupt nur zwischen den Zeilen von Fachleuten erkannt werden. Das klassische Beispiel hierfür ist der ewige Kampf zwischen Genauigkeit und Geschwindigkeit.
Häufig fragt man sich, ob die Mühe für eine Berechnung überhaupt lohnt, wenn die Zeitschiene des Auftraggebers so eng ist, dass das Ergebnis genauso gut als das Produkt zweier Postleitzahlen mit dem aktuellen Datumsstempel generiert werden könnte.
RANS Gleichungen erhöhen Stabilität und Geschwindigkeit
Einen Ausweg aus diesem Dilemma versuchen einige Softwarehersteller damit zu lösen, indem sie bei der mathematischen Formulierung des Problems sog. RANS (Reynolds-Averaged-Navier-Stokes-) Gleichungen einführen. Diese enthalten zur Vereinfachung kleinskaliger Turbulenz einige Annahmen in Form von sog. Turbulenzmodellen, die in einer direkten CFD Berechnung nicht enthalten sind.
Diese Turbulenzmodelle haben den Zweck, besonders feine und turbulente Strömungen nicht direkt berechnen zu müssen, da dies sehr zeit- und ressourcenintensiv ist. Turbulenzmodelle ersetzen diese feinen turbulenten Strömungen durch eine lokal gemittelte Größe wie die z.B. sog. „Turbulenzintensität“ und deren Schwankungsbreite oder deren Abklingverhalten. Damit ergibt sich ein enormer Vorteil:
Wenn man diese sehr feinen Verwirbelungen nicht exakt berechnen muss sondern nur ihre mittlere Intensität benötigt, kann das gewählte Netz deutlich gröber ausfallen. Das spart Unmengen an Zeit und Ressourcen, wirft aber berechtigterweise die Frage auf:
Wie gut bildet das gewählte Turbulenzmodell tatsächlich noch die Realität ab?
Um diese Frage zu beantworten berechnen Softwarehersteller oftmals Referenzprobleme und verifizieren diese mit Hilfe von Messdaten. Soweit so gut. Die Berechnungsergebnisse bilden diese Referenzprobleme oft sehr gut ab und verdeutlichen so die Leistungsfähigkeit der jeweiligen Software (für genau diese Problemstellung!).
Was aber ist, wenn meine Strömungssimulation mit Randbedingungen klarkommen muss, die weit ab der gewählten Referenzprobleme liegen? Wie kann ich mir sicher sein, dass die Software hier auch richtig rechnet? Die Antwort ist einfach: Im Grunde gar nicht. Ich kann eigentlich nur hoffen, dass sie die Realität ähnlich gut abbildet wie für die Referenzproblemfälle, da das Turbulenzmodell oder zusätzliche Vereinfachungen der Strömungssimulation in einer unbekannten Anwendung eine „black box“ darstellt.
Es gibt weitere Vereinfachungen der strömungsmechanischen Prozesse, die meist das Ziel haben die Berechnung oder den Modellaufbau zu vereinfachen und zu beschleunigen. Manch einer wird vielleicht behaupten wollen, es handelt sich bei solchen Berechnungsverfahren gar nicht mehr um eine „echte“ CFD Berechnung. Aber geht es nicht bei jedem Simulationsverfahren um die möglichst genaue Abbildung der Realität? Wenn diese durch eine „echte“ CFD zustande kommt ist das gut, wenn diese aber auch durch vereinfachende Annahmen in einem Bruchteil der Zeit möglich ist, ist das (abseits der Grundlagenforschung!) für mich zumindest ein großer Gewinn.
Trotzdem gilt natürlich: Je mehr dieser Annahmen und Berechnungsvorschriften in einer Software hinterlegt werden, umso mehr muss die Frage erlaubt sein, ob und in welchem Bereich der Randbedingungen die Ergebnisse die Realität widerspiegeln.
Abgleich mit Messungen wo möglich immer sinnvoll
Streng genommen erfordert deshalb jede Strömungssituation, die von den verwendeten Referenzbedingungen abweicht, entweder die direkte (sehr aufwändige) CFD Berechnung des Problems oder den (ebenfalls aufwändigen) Abgleich der Ergebnisse mit Prüfstandsmessungen.
Was schätzen Sie, wie viele Auftraggeber haben die Zeit und das Geld für diese Art von Versuchen? Sie ahnen es… So etwas wird praktisch nur in der Grundlagenforschung durchgeführt, wenn Leib und Leben von Menschen an den Ergebnissen hängen oder aber sehr sehr viel Geld.
Aber zur Beruhigung: In den meisten Fällen wird ein gutes Turbulenzmodell in dessen Gültigkeitsbereich auch mit Problemstellungen fertig, die nicht vorher getestet und verifiziert wurden, vorausgesetzt, der Anwender weiß, was er tut. Das k-epsilon Turbulenzmodell beispielsweise hat sich für viele Industrieanwendungen seit Jahrzehnten bewährt. Wäre dies nicht der Fall, würde die Software und das Modell schnell vom Markt verschwinden. Trotzdem bleibt es aber dabei: mit jeder zusätzlichen Annahme für ein Problem wird der Gültigkeitsbereich der Lösung eingeschränkt.
In anderen Worten: Die Berechnungsergebnisse sind nur dann korrekt, wenn alle getroffenen Annahmen in der Realität auch zutreffen.
Lösung immer hinterfragen, Randbedingungen in der Realität prüfen
Dieser Tatsache sollte man sich bei der Durchführung von Strömungssimulationen immer wieder stellen. Hinterfragen Sie immer die Lösung! Gibt es einfache Möglichkeiten zur Prüfung? Ist das Ergebnis plausibel? Sind alle Annahmen an das gewählte Modell durch die Problemstellung auch wirklich erfüllt? Treten unerwartete Phänomene auf? Gibt es dafür einen physikalischen Grund, oder liegt die Ursache vielleicht im Berechnungsalgorithmus?
In meinem nächsten Eintrag möchte ich diese Gedanken vor dem Hintergrund einer ganz einfachen, praktischen Aufgabe betrachten. Nämlich der Frage nach der optimalen Netzgestaltung für einen durchströmten Kanal, wenn – wie zuvor beschrieben – viele solcher Zusatzannahmen in einer Software hinterlegt sind.
Reichen hier nicht strenggenommen bereits ein paar Zellen aus, um das Problem genau genug zu beschreiben, oder gilt auch hier: je feiner, desto besser?
Nachdem ich im ersten Teil ein paar grundlegende Gedanken formuliert habe, möchte ich diese in diesem zweiten Teil an einem einfachen Beispiel etwas näher ausführen. Obwohl das Beispiel bewusst einfach gehalten ist, ergeben sich einige interessante Ergebnisse.
Beispielberechnung 180° Rohrbogen
Nehmen wir als Beispiel eine einfache 180° Rohrbiegung wie in Abbildung 1.

Dieses Rohr soll nun durchströmt werden und der Druckverlust als ein einfaches Ergebnis der Strömungssimulation in Abhängigkeit der Randbedingungen (Temperatur, Volumenstrom bzw. Massestrom, Medium, etc.) berechnet werden.
Wie komme ich nun „am schnellsten“ zu einer „akzeptablen“ Lösung, wenn ich weiß, wie im ersten Beitrag beschrieben, dass eine Vielzahl von Vereinfachungen das Strömungsmodell bestimmt? Eigentlich müsste ich fragen: Wieviel Zeit steht mir zur Verfügung und wie groß darf die maximale Abweichung vom exakten Ergebnis werden? Die letzte Frage ist besonders schwer zu beantworten, da ich das tatsächliche, exakte Ergebnis ja gar nicht kenne, solange ich nicht absolut saubere Referenzmessungen am Prüfstand durchführen kann.
Laminare und turbulente Vergleichsrechnung
Für dieses Beispiel möchte ich einmal den vollständig laminaren Fall und einmal den vollständig turbulenten Fall dieser Rohrdurchströmung betrachten. Denn für beide Fälle kann der Druckverlust händisch nach gängigen VDI Vorschriften berechnet werden. Dazu zunächst noch alle verwendeten Randbedingungen:
- Fließmedium: Wasser bei T = 20,0 °C
- Rohrdurchmesser d = 30,0 mm
- Rohrkrümmungsradius r = 120,0 mm
- Gitterparameter a des Netzes: Variiert zwischen 30 mm und 0,3 mm
- Wandrauigkeit: 0,04 mm (neues, sauberes, gezogenes Kupferrohr)
- Reynoldszahl laminar: 659 (entspricht Strömungsgeschwindigkeit von ca. 0,2 m/s)
- Reynoldszahl turbulent: 164744 (entspricht Strömungsgeschwindigkeit von ca. 5,0 m/s)
- Weitere Voraussetzung: vollständig ausgeprägte Strömung am Einlassprofil
- Wahl des Turbulenzmodells: „Turbulenzintensität und –Länge“
- Werte für Turbulenzintensität I = 2% und Intensitätslänge I_L = 0,00033m (=vorgeschlagene Standardwerte)
- Vollständig kartesisches Netz
Das erwartete Ergebnis für den Druckverlust zwischen Ein- und Ausgang des Rohrbogens für den hier betrachteten laminaren Fall beträgt 0,56 Pa und für den turbulenten Fall 1872 Pa. Diese Ergebnisse spiegeln empirische Erfahrungen wider und stellen selbst keinen Anspruch auf absolute Richtigkeit, werden in diesem Rechenbeispiel aber als „richtig“, da empirisch belegt, angesehen. Der wahre Wert für dieses Strömungsbeispiel kann jedoch tatsächlich auch ein etwas anderer sein.
Hat das Netz einen großen Einfluss auf das Ergebnis?
Nun stellt sich noch die Frage nach der Netzauflösung. Je feiner das Netz, umso länger dauert die Berechnung und umso mehr Speicher wird benötigt. Man würde jedoch erwarten, dass sich das Ergebnis mit steigender Netzfeinheit näher an den erwarteten Wert angleicht, also genauer wird.
In der hier von mir für diesen Beitrag verwendete Software kann zudem zwischen Fluid und Festkörperbereich innerhalb einer Zelle über die Verwendung sogenannter SmartCells und Wandfunktionen unterscheiden. Auch diese Wandfunktionen enthalten Zusatzannahmen über die sich ausbreitende Strömung in Wandnähe, erleichtern die Vernetzung des Modells jedoch erheblich. Es handelt sich aber wie zuvor beschrieben um Zusatzannahmen zur Beschleunigung der Berechnung, die in einer direkten CFD nicht vorhanden sind.
Jetzt stecken also bereits zwei empirische Näherungen in dem der CFD hinterlegten Gleichungssystem: die RANS Gleichungen und die Wandfunktionen (in der Tat sind es noch ein paar mehr, aber das soll uns hier zunächst nicht weiter stören). Wie gut funktioniert das in der Praxis noch? Wie schnell ist es wirklich? Und vor allem: Wenn wandnahe Turbulenzen nur noch zeitlich gemittelt und in Wandfunktionen versteckt werden, wieviele Zellen benötigt man nun noch innerhalb eines Fluidbereiches für ein genaues Ergebnis?
Hierzu schweigt der Hersteller und verweist stattdessen auf die unterschiedliche Behandlung von „dünnen“, „dicken“ oder mittleren Grenzschichten. Es existiert ein Referenzbeispiel eines CPU Kühlkörpers in einem Whitepaper des Herstellers, dass gute Berechnungsergebnisse schon mit 1-2 Zellen pro engem Strömungskanal ergibt. In einem anderen Referenzbeispiel werden 15 Zellen über einem Kanal verwendet. Der Softwaresupport antwortet telefonisch auf diese Frage mit „ca. 5 sollten es erfahrungsgemäß schon sein“. Ja wie denn jetzt? Und gilt das immer, oder nur für bestimmte Randbedingungen?
Laminarer und turbulenter Fall unterscheiden sich in Geschwindigkeit und Genauigkeit für das selbe Referenzproblem bereits in so einem einfachen Fall
Betrachten wir diese Frage anhand unseres kleinen Beispiels. In Abbildung 2 habe ich den relativen Fehler der Simulationsergebnisse bezogen auf den Wert nach VDI-Berechnung aufgetragen über der Anzahl der Zellen, die im Rohrdurchmesser nebeneinander liegen können. Das ganze einmal für den laminaren und einmal für den turbulenten Fall.

Idealerweise sollten beide Kurven auf der 0-Linie enden. Im turbulenten Fall passiert dies auch schon für kleine Netzzellenzahlen, für den laminaren Fall erst bei größeren, für ganz große Netzzellenanzahlen bewegt sie sich wieder etwas von der Nulllinie weg.
Was auch auffällt ist: Trotz der Verwendung einiger, in der direkten CFD nicht vorhandenen Annahmen bezüglich der Turbulenz und Randschichten funktioniert dieser Ansatz erstaunlich gut. Bereits ab ca. 4-5 Zellen im Durchmesser der Rohrbiegung werden für die turbulente Strömung Lösungen erhalten, die weniger als 5 % fehlerbehaftet sind.
Für die laminare Strömung liegt dieser Wert höher und für gute Ergebnisse muss hier auch ein feineres Netz gewählt werden. Trotzdem mündet der relative Fehler nicht auf der 0-Linie, was möglicherweise auch am konservativen Charakter der VDI-Berechnungsmethode, also einem potentiell etwas zu hohem Referenzwert, liegt.
Diese Abweichung kann jedoch auch am „Abschneiden“ der Sekundärströmung am Rohrausgang liegen, denn das Modell hat in diesem Fall bewusst keine Einlauf- und keine Auslaufzone. Mit der Randbedingung „Drucköffnung“ direkt am Rohrbogenende wird die Ausprägung der Sekundärströmung gestört, was zu Fehlern bei der Bestimmung des Druckverlustes führen kann. Korrekt wäre hier also das Mitbetrachten einer Einlauf- und Auslaufzone und das anschließende Auswerten der Druckunterschiede am exakten Rohrbogenein- und –ausgang.
Außerdem gibt es einen relativ plötzlichen Umschlag von einer Untertreibung des Referenzwertes zu einer Übertreibung. Bei genauerer Betrachtung wird klar, dass dieser Umschlag mit der Ausprägung der Sekundärströmung im Rohrbogen zu tun haben könnte. Diese wird erst ab ca. 8 Zellen im Rohrdurchmesser qualitativ so beschrieben, wie sie erwartet wird. Dies spricht für die Implementierung von wenigstens 8 Zellen pro Kanal für laminare Strömungen.
Für die turbulente Variante wird die Sekundärströmung sogar erst ab ca. 20 Zellen pro Rohrdurchmesser qualitativ richtig und mit zunehmender Zellenzahl besser erfasst.
Gibt es eine „optimale“ Zellenanzahl über dem Strömungsquerschnitt?
Möchte man nun zusätzlich wirtschaftlich arbeiten, bleibt noch die Frage nach der Rechenzeit. Dazu habe ich die Zielfunktion O erstellt, die umso größer wird, je kürzer die Berechnungszeit wird und je kleiner der relative Berechnungsfehler wird. Sie ist also umso größer, je schneller und genauer die Berechnung ist. Normiert man diese Zielfunktion, kann man den laminaren und den turbulenten Fall gut miteinander vergleichen. Das ist in Abbildung 3 gezeigt.
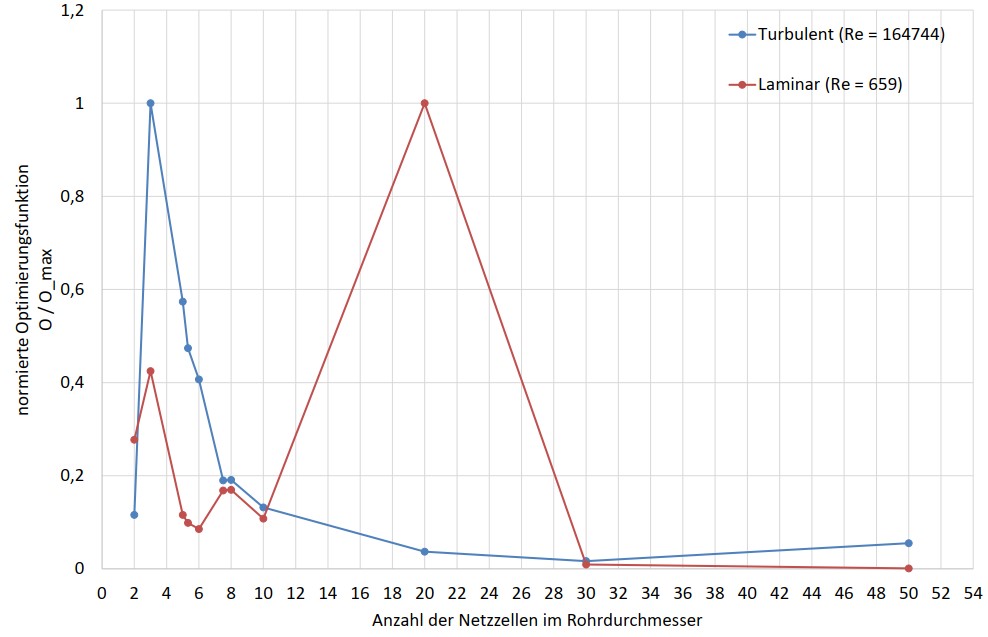
Die Abbildung zeigt ein Maximum der Optimierungsfunktion für den turbulenten Fall bei 3 Zellen im Durchmesser. Auf meiner Maschine lief die Berechnung dieser Simulation innerhalb von 5 s ab und ergab einen relativen Fehler von 13 % Abweichung vom VDI Wert. Kein schlechter Wert für so eine schnelle Berechnung.
Für den laminaren Fall sind es in diesem Fall jedoch 20 Zellen im Rohrquerschnitt, da hier der Referenzwert ziemlich genau getroffen wird. Hier rechnete meine Workstation 119 s bei einem relativen Fehler von <1 %.
Zum Vergleich: Die Berechnung bei 50 Zellen im Durchmesser dauerte bereits knapp 50 min und lieferte für beide Fälle keine deutlichen Verbesserungen. Probehalber habe ich noch einen Datenpunkt bei 100 Zellen im Durchmesser erstellt. Die Berechnung lief über 11 h und brachte ebenfalls keine Verbesserung in der Genauigkeit.
Was ist also unser Fazit?
Was ist also unser Fazit? Ich würde es vorsichtig so formulieren: Spezielle, auf Geschwindigkeit optimierte CFD Software kann sehr gute Resultate liefern. Man muss allerdings mit dem „black box“ Charakter solcher Systeme leben und sich dessen auch immer bewusst sein. Überlegungen wie diese hier sollten immer durchgeführt werden, um auch bei komplexeren Strömungssimulationen ein gutes Gefühl bei den Ergebnissen haben zu können.
So ist es durchaus gut zu wissen, dass man bei der hier verwendeten Software für eine laminar erwartete Strömung die Zellenzahl über dem Strömungskanal etwas höher als für reine turbulente Strömungen wählen sollte, auch wenn der laminare Fall scheinbar einfacher ist. Die Hilfe, die Referenzbeispiele und die Whitepapers des Herstellers schweigen sich hierzu nämlich (vermutlich bewusst) aus. Trotzdem war die Empfehlung des Softwaresupports hier durchaus brauchbar.
Ähnliche Simulationsexperimente werden sicher in nächster Zeit folgen. Es sind schließlich noch viele Fragen offen, wie z.B. der Einfluss der Turbulenzmodellparameter, oder ob sich unser Beispiel genauso verhält, wenn wir statt erzwungener eine freie Konvektionsströmung annehmen. Und und und..
Schaut gern mal wieder vorbei und bis dahin wünsche ich frohes Experimentieren.


